Problem Statement
King Arthur loves to invite the knights over to his round table for dinner, and often times, holds a contest for them. For the contest, King Arthur has the knights come and sit in a chair. He goes up to a knight and says, "you're in" then moves on to the next chair and says, "you're out". He continues until there is only one knight left, and they become the winner. How can you determine which one is the winning seat without being aware of how many knights there are? Create a formula / rule.
Process
|
In the beginning of the problem, we were tasked to first ask/write down initial questions we had that we could then communicate back to our group and make sense of the problem better. The first questions I found myself writing down were:
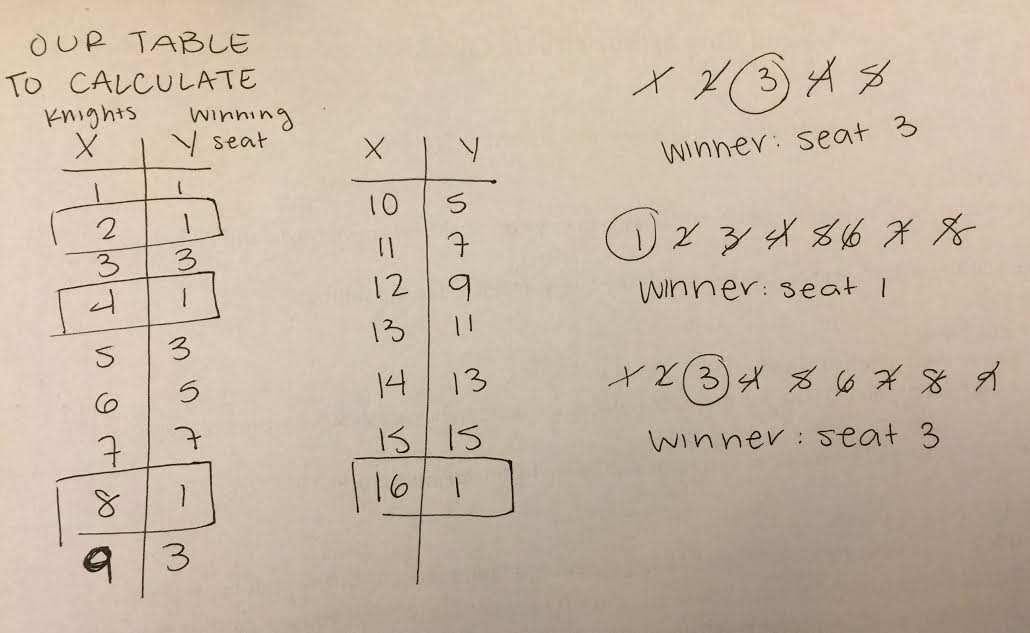
- How do we create a formula to include the missing knights as well? - How many chairs were unoccupied? - How many knights were missing? - What do we need? (maybe the number of times he went around the table would be helpful) I realized that these questions didn't help at all because they weren't important / needed to solve the problem. As long as you knew exactly what the problem was saying, then you could figure out how to solve it without the information you weren't given. Our group then started to communicate and share basic ideas. I shared out my questions, and they explained how I didn't need to answer those to solve the problem. Then, Ivanna went on to explain her method, of using an x-y table to see if there was a pattern and have an easier way of tracking the winners. |
Solution
|
Through this method, we found that there was a pattern that every time a knight won, it was in an odd numbered seat. That meant that all our winners would be odd seats, even if there are an even amount of knights sitting in chairs.
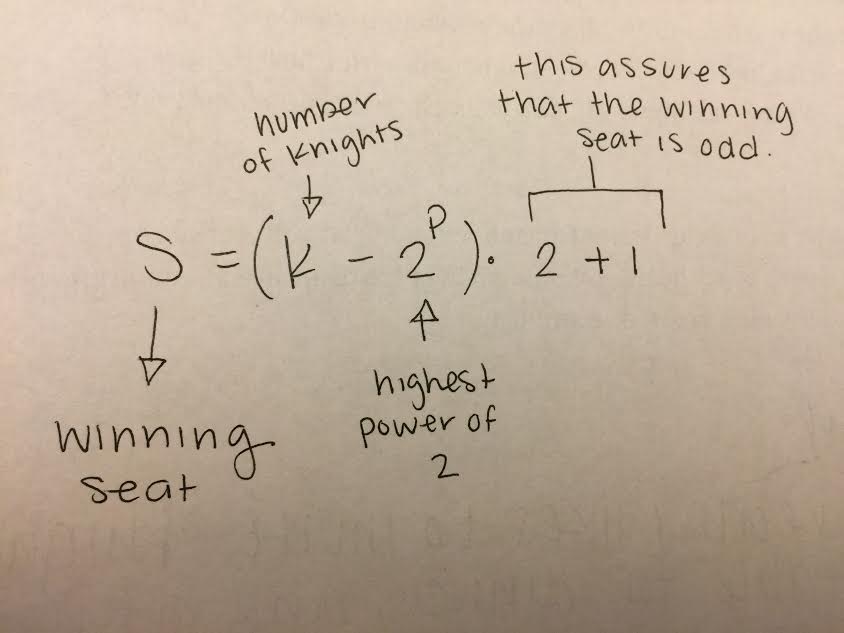
( The examples on the right of the table show that our numbers match the ones we found in the table ) After working on the problem together and trying to solve it, we finally found an equation. The equation was written out as seen on the right.
S = K - 2^P x 2 + 1 What each number / variable represents are: - S is what we're trying to find, which is the winning seat - K is the number of knights sitting in chairs - 2^P are the powers of 2 that fit into the number of knights we have - x2 + 1 is what we need to then add to the number we get in the parenthesis to assure that we get an odd "chair" number With this equation, we then found it easier to solve the problem, and eventually, when we tried it out in real life, it worked and we were able to get the winning seat. |
Evaluation / Reflection:
In this problem, what pushed my thinking the most was trying to find out basic steps for the solution. In the beginning, I wasn't sure what we were supposed to do with the problem and how we were going to go about that, so I think trying to find basic first steps and working with my group was what pushed my thinking. I think I was challenged in trying to understand the equation the first time my group explained it to me. I'm not exactly the best when it comes to Math, but after having my group explain it and having them solve it with me for the first time, it was a lot easier to understand and apply the equation when trying to figure out the winning seat. I can recognize when I need help or when I'm struggling because I get stuck and I realize I can't go on any further when figuring something out. These past few months, I haven't been afraid of asking for help because I know that by doing that, I'm also contributing to my group and helping others that might not understand it in the beginning. I also feel confident in helping those around me and helping them understand something when they might be confused or when they're not sure about a certain step we might be taking at the moment. In the beginning, I feel like my group really helped me and others try to better understand the problem and we first tried answering any questions that we had or anything we were confused about. We never really let anyone fall behind and we always asked each other if we understood, and if we didn't, we tried to help them the best we could. Our group quiz definitely helped me a lot to try and better understand the problem on my own. I feel a lot more confident about the problem and how to go about solving it now that I was able to work with my group. I feel like I deserve an +A because I definitely tried to contribute the best I could to the problem, and the first time Mr. Carter asked me to explain the method Ivanna showed us, I was able to explain it and make sense of it for myself at the same time.