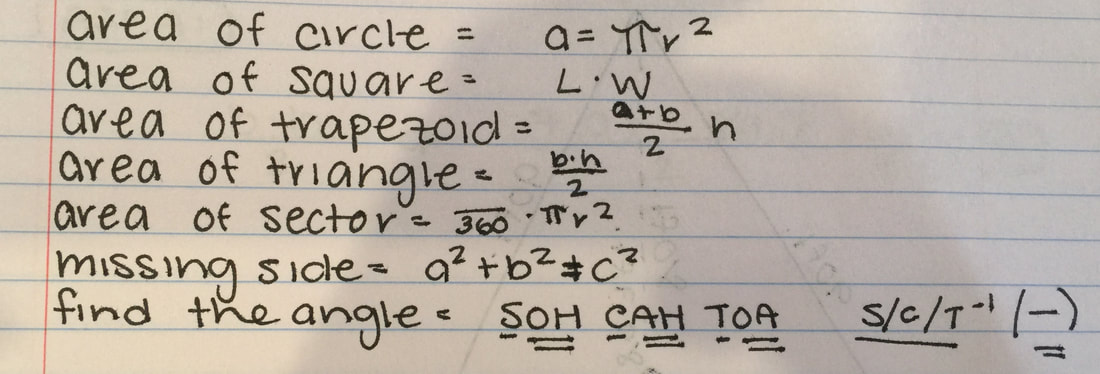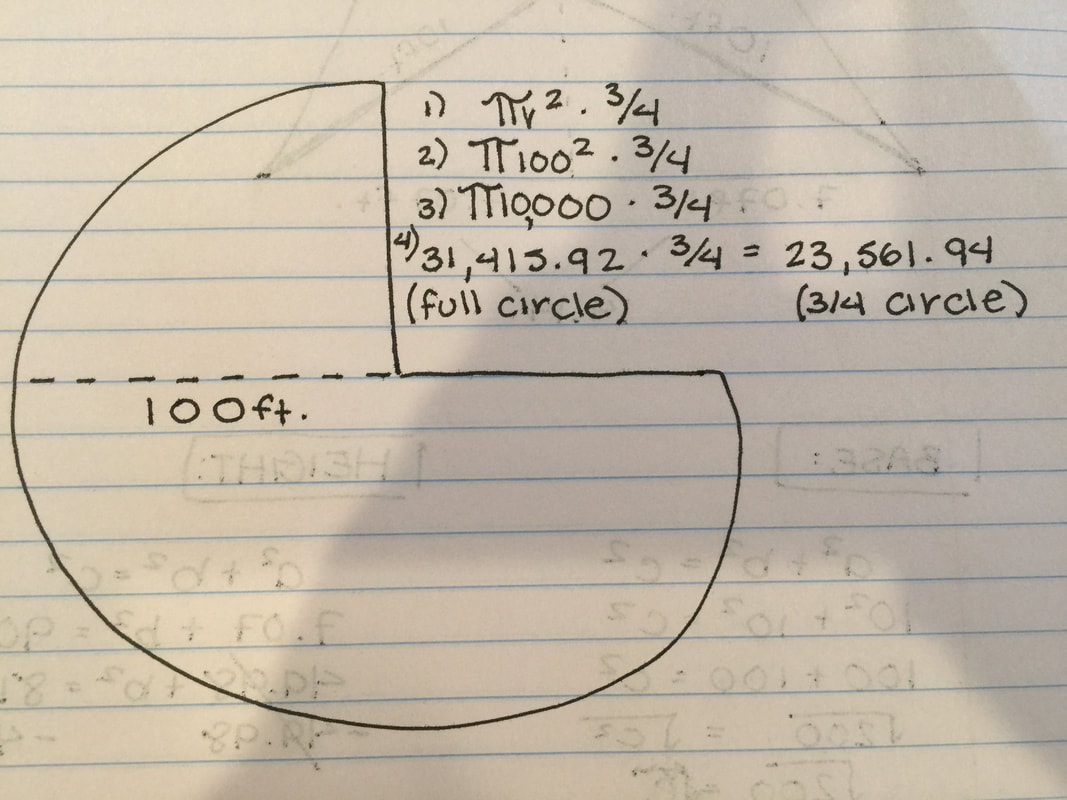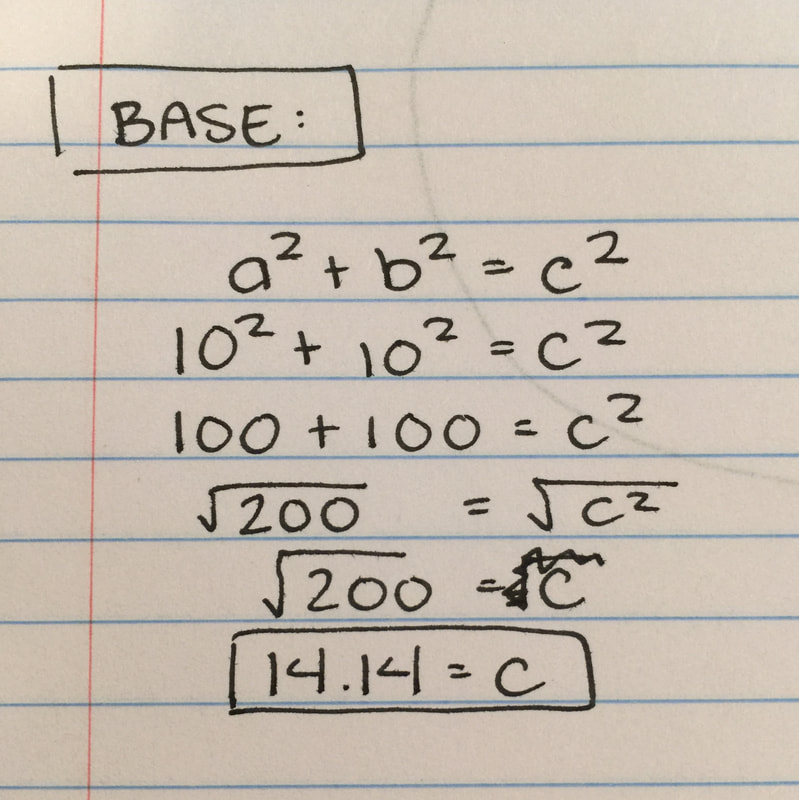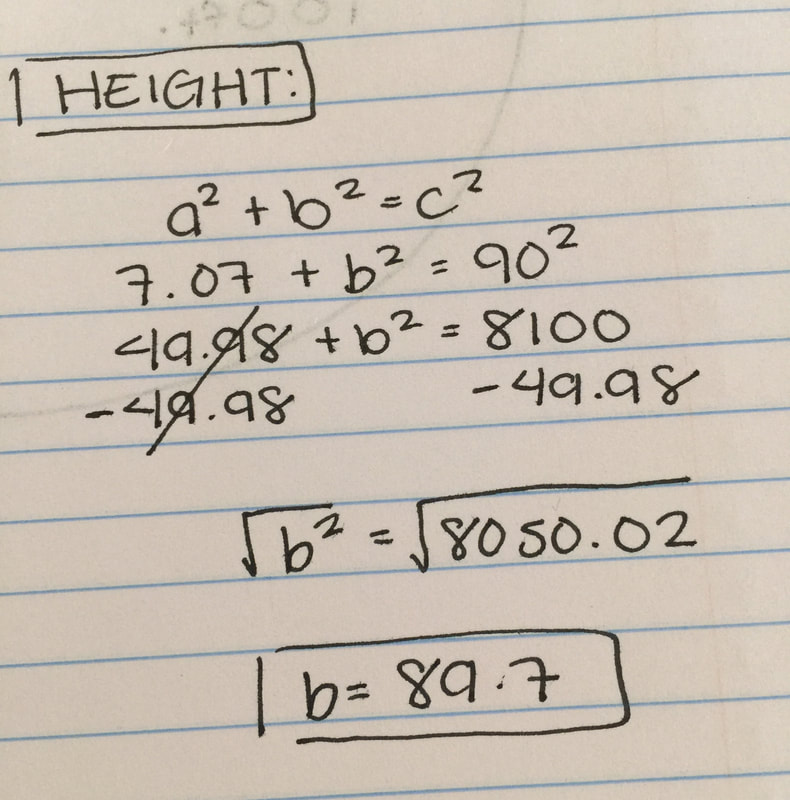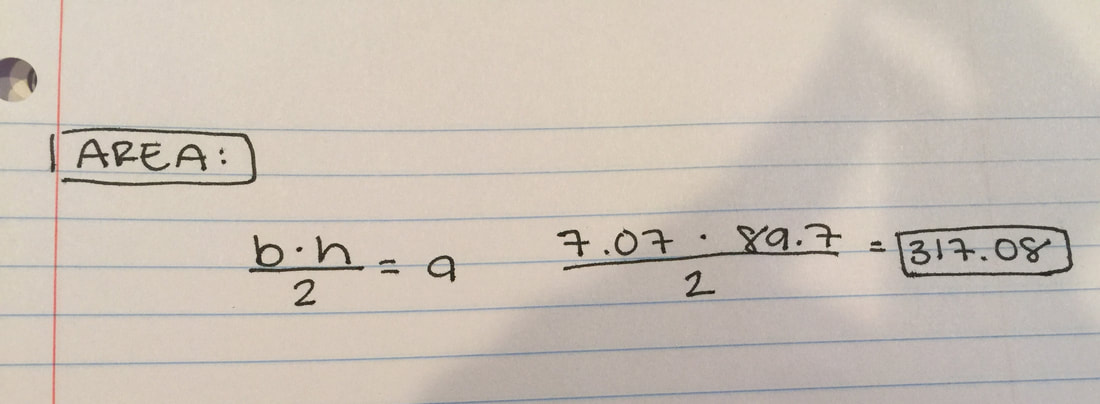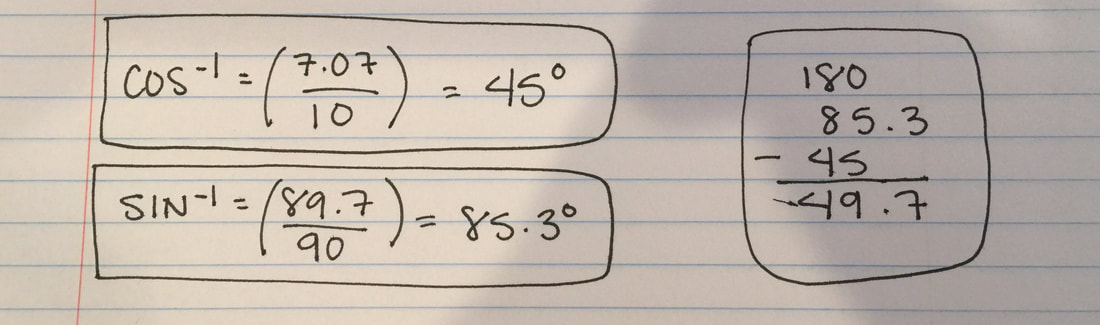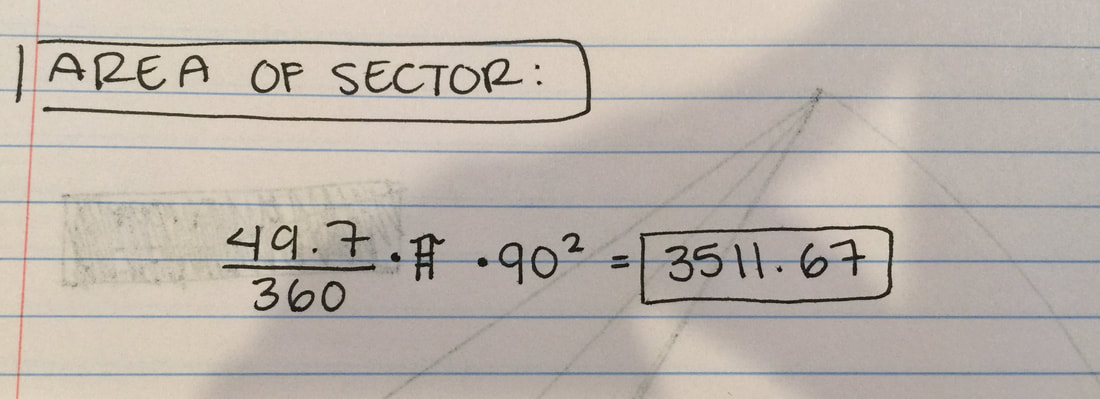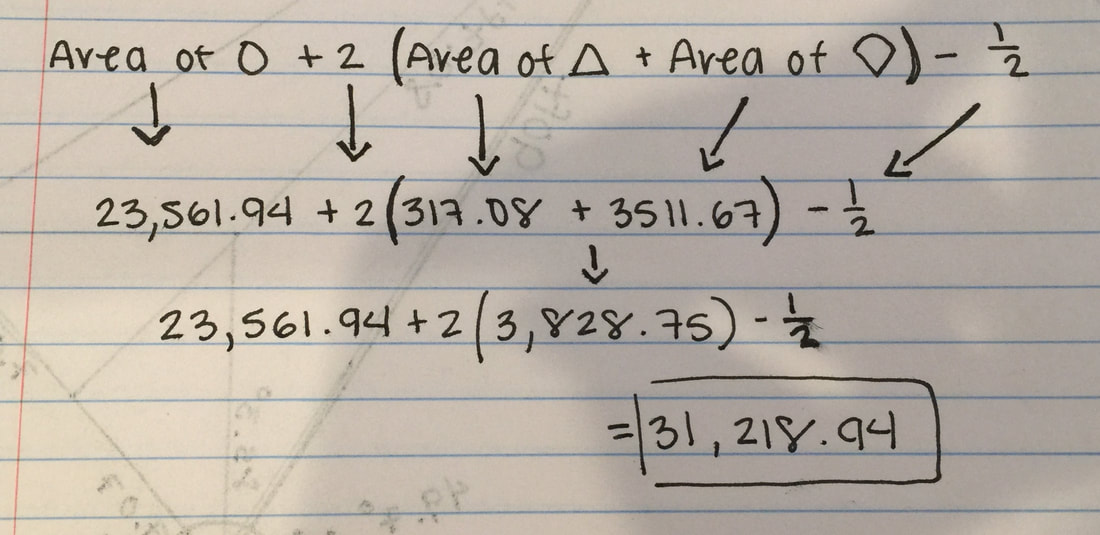September 29th, 2017
Problem Statement
In the first few weeks of school, Mr. Carter gave us a problem we would be looking over for 3 weeks of the semester, while we worked on another project, The Growth Mindset Project. The question seemed simple, yet required various different equations and methods to solve. We would be working in groups, to teach each other and answer questions we might know for our other classmates. This was the problem:
There's a cow that has been attached with 100ft rope to a barn that measures 10ft x 10ft. Knowing these measurements, how much grass can the cow reach and how far can it go until it runs out of rope?
There's a cow that has been attached with 100ft rope to a barn that measures 10ft x 10ft. Knowing these measurements, how much grass can the cow reach and how far can it go until it runs out of rope?
Process
|
For my process, in the beginning I tried to draw a diagram by myself, which resulted in me just being confused and mixing up the measurements. In my group, we tended to stick together, so if one of us was confused, everyone had to stop and help that one person. So no one was left behind during this activity. It really helped me a lot to have my group mates willing to help me if I need it and answer any questions I might have.
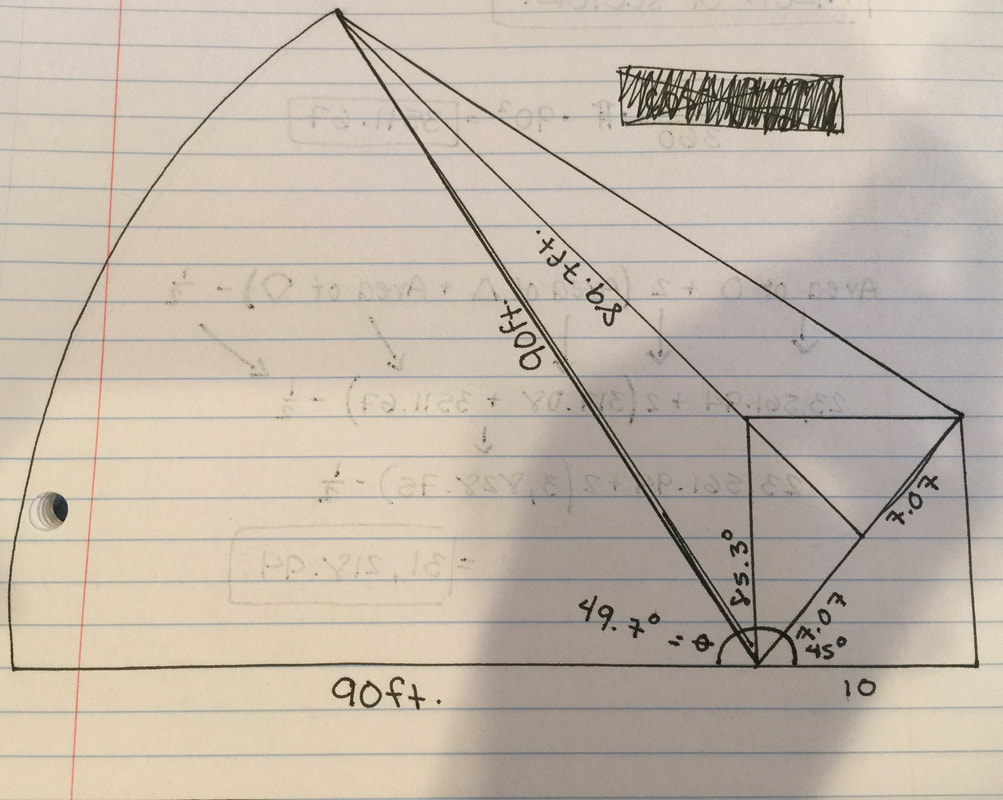
We started drawing different diagrams as a group, first doing the little box to represent the barn and then adding a line for the rope and a point for the cow. From here, we discussed with each other that if the cow were to go to the right, it would have 100 ft of rope to wander with and if it went left, it would have 90, because it used up 10ft (that was one side of the barn) and the rest is what's left of the rope. From the information we gathered, and when we talked as a whole class, we figured that if it were to be a shape, it would be 3/4 of a circle. From there, we started our diagram, taking the 3/4 of a cirlce and applying it to the rest of the drawing we had been making. That immediately gave us a good view of where the cow could graze with 100ft. of rope without the number going down. From here, we decided that if it were to walk father than the 3/4 circle, the amount of rope would decrease, and it would no longer be a full circle, but a 3/4 circle with the last quarter of it dipping down into itself. This made sense when we drew it as a diagram. (slide 10) |
|
Dimensions Required:
- 10ft. x 10ft. Barn
- 100ft. Rope
- Angle of Triangle
- Angle of Sector
- Base of Triangle
- Height of Triangle
- Area of Triangle
- Area of Sector
- Area of Circle
- 100ft. Rope
- Angle of Triangle
- Angle of Sector
- Base of Triangle
- Height of Triangle
- Area of Triangle
- Area of Sector
- Area of Circle
|
After this, as a group, we started looking at various different equations. Mr. Carter told us that we couldn't figure out the "dimple" shape because it was a shape we were unfamiliar with. So, Mr. Carter, with the help of the different packets he gave us to work on, we were able to find basic equations to find the area of different shapes. Trapezoids, circles, triangles, and sectors. We also looked at the equations for angles and how to find them. This was definitely going to help us when it came to putting the equation in the end together.
|
|
With these equations ready for us, we first needed to find the Area of our Circle. Since the circle is not full, we knew we needed to make an adjustment to our equation for the circle. The full equation for a complete circle is: π r^2.
R = Radius of The Circle = 100 (how far the cow can go) Now, the full equation would be replaced like how it's shown on the right. In the end, we would multiply our final area (which would be for a full circle) with 3/4 since we only needed the area for 3/4 of the circle. Our final area was 23,561.94. |
FULL EQUATION:
π r^2 x 3/4 π 100^2 x 3/4 π 10000 x 3/4 31,415.92 x 3/4 = 23,561.94 |
|
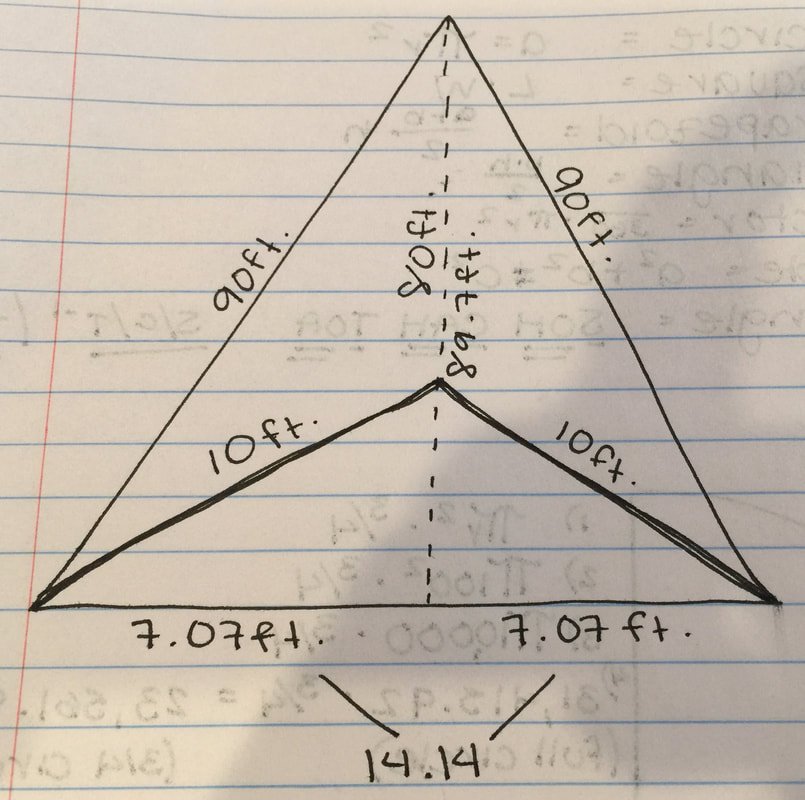
Our next step was to then find the area of our triangle. By itself, it looked foreign to us, because it was shaped like a paper airplane and not an actual triangle. So, we decided to combine half of the barn with the "paper airplane" and create a full right triangle.
Now, with our new triangle, we first needed to find the base. For this, we used the formula: A^2+B^2=C^2. C = hypotenuse A = one side B = other side (opposite from A) By plugging in the numbers that we already know (10ft & 10ft) into our variables (A & B) we were able to find the base, which was 14.14. After this, we needed to find the height of the triangle, so we divided the base in half, seeing as we only needed half of the triangle to find the height. By dividing the triangle, we found 7.07, and we only needed this since both sides of the triangles are the same, and in the end, we get the area (which will be the same). For the height, we needed plug in 90ft into C, 7.07 into A and solve for B. It would look like this: 7.07^2 + B^2 = 90^2. In the end, it should give you the height of 89.7. And for the final step, to find the area. For this, we need the formula B x H/2 = A. For this, you divide by 2 because you are using half of the barn in the triangle and we only need the "paper airplane" area. The final area is = 317.08. |
|
The final step is to find the area of the sector. So for this one, we need to find the angles first, and we would use the formula Sin, Cos, or Tan^-1 (SOH CAH TOA). If you know what the formula is, it makes everything easier if you know what SOH CAH TOA means. After we plug the numbers in, we need to make sure that there's a negative sign where the 1 is since we are finding the angle and not the side.
SOH = sin is opposite/hypotenuse CAH = cos is adjacent/hypotenuse TOA = tan is opposite/adjacent On the right is how (as a group) we found the angles for the diagram. Since the line on the bottom is a straight line, it means it's 180 degrees, so all we had to do is subtract the two angles we found from 180 and we got 49.7 degrees, which equals the angle for the sector. So now, to find the area of the sector (on the right), we needed to divide the angle of the sector (49.7) by (360), which is a full angle so we can see what percent of the circle we are using to find the area which is .138. Then, we need to multiply by the area of the circle (π90^2) and you will finally get the area of the sector! |
This is the final step. In order to find the full and complete area that the cow can graze, we need to put all the information we gathered above together into one complete equation. Which means, we need to use this equation.
Area of Circle + 2 (Area of Triangle + Area of Sector) - 1/2
The reason for the +2 is because there are 2 sides to the triangle and sector (and we multiply it by 2). The 1/2 is for the half of the barn we used for the triangle that we are going to get rid of. We don't need that half since we are only looking for the area of the full "dimple shape" and not the barn. The final answer is at the bottom!
Area of Circle + 2 (Area of Triangle + Area of Sector) - 1/2
The reason for the +2 is because there are 2 sides to the triangle and sector (and we multiply it by 2). The 1/2 is for the half of the barn we used for the triangle that we are going to get rid of. We don't need that half since we are only looking for the area of the full "dimple shape" and not the barn. The final answer is at the bottom!
Evaluation/Reflection:
I feel like this problem really helped me speak up more and ask questions, especially since I didn't do this as much last year. Plus, in this group, I felt really comftorable admitting that I needed help and asking a lot of questions, because I realized that a question that I had, maybe someone else had it too so we were able to learn at the same time and explore different questions we might have. I honestly think I learned a lot about the different formulas needed for this problem than I used to know, because we worked in groups and with each other, rather than having to watch the teacher do the problem on the board and having to do it by myself. It was easier and I was able to get the insight of my group members. The group quiz really affected me positively because during it, I was able to look at the formulas differently and actually understand them with the help of my group. Each question we asked each other helped us in some way. There was a time where Alani wrote a formula down that was backwards and when I asked a question, she realized her mistake and fixed it. From here on, we looked at our process and were able to figure out how to find our solution, together. No one was left behind during the whole quiz and the rest of the problem. We always made sure that we stuck together and understood everything before moving on. If I were to grade myself, I feel like I would give myself an A because I was able to understand the topic and all the formulas, as well as help my group mates and ask a lot of questions whenever I was confused. I made sure that if I didn't understand something, I immediately asked for help, and if someone else didn't understand, I would try and help them as best as possible. The day after we had the lecture with Mr. B about the different formulas needed to figure out our "dimple shape", Alani had come back from being absent. She immediately asked for my help on what we had learned prior to that day and I tried to help her as best as possible. I showed her my notes and lent them to her so she could go over them. She asked me questions, and using knowledge from the day before, I tried to answer them. The ones I didn't understand, I told her I wasn't sure and we asked an adult about that step. But we made sure we both understood it because it was definitely confusing looking at something from a day before and trying to understand every single thing about the formulas. So we definitely tried to help each other.